Cython Examples: Random Sampling and Latent Dirichlet Allocation

Posted on 17 Aug 2019

Introduction

I have been working on a project implementing a sort of human-in-the-loop version of Latent Dirichlet Allocation (LDA). Due to constraints of this project, I needed an implementation of LDA that used collapsed Gibbs sampling, and ran quickly as well. Needing other access to the internals of the model as well caused me to look into implementing LDA myself. The need for speed landed me at looking into implementing the model in Cython, which I learned is a little tricky to get working exactly right. So I put together an introduction to getting up and running with Cython, including examples to write a random sampler and the code needed for the collapsed Gibbs sampling algorithm for LDA.

What is Cython?

\[\fbox{$Python \subseteq Cython$}\]

Cython can refer to either the programming language or the static compiler.

From cython.org:

Cython is an optimising static compiler for both the Python programming language and the extended Cython programming language (based on Pyrex). It makes writing C extensions for Python as easy as Python itself.
⋮
The Cython language is a superset of the Python language that additionally supports calling C functions and declaring C types on variables and class attributes.

Cython gives a way to write code similar in syntax to Python, that can be converted to C/C++ code, which can be called easily with Python.

The setup

We need

Cython
C/C++ compiler

For Cython:

pip install Cython

conda install cython

For C/C++ compiler on Mac:

A little hairy. First, install Apple’s Xcode: xcode-select --install.

For recent versions of MacOs, we need to do the following from this comment to a stackoverflow question https://stackoverflow.com/questions/52509602/cant-compile-c-program-on-a-mac-after-upgrade-to-mojave:

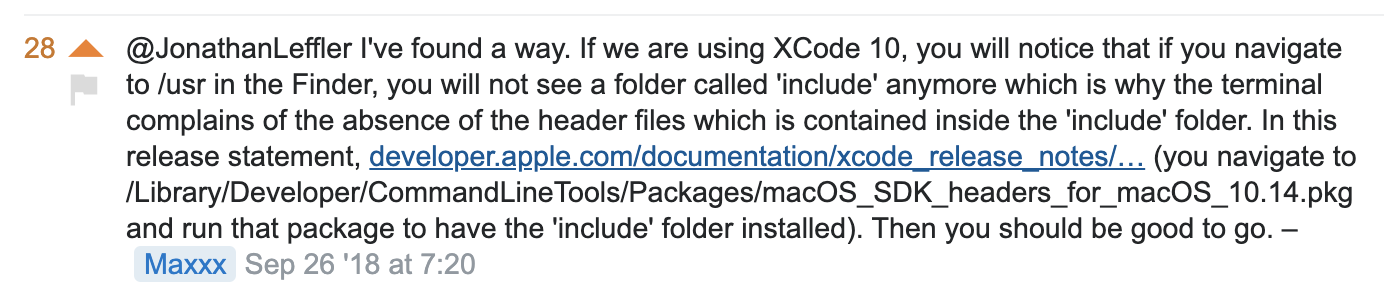
Cython in a notebook

Running Cython in a notebook is fairly straightforward. To get started, we need to run a cell with this code.

%load_ext Cython

Next, we’ll go through some examples of simple functinos summing integers.

Summing integers

def sum_py(x):
    y = 0
    for i in range(x):
        y += i
    return y

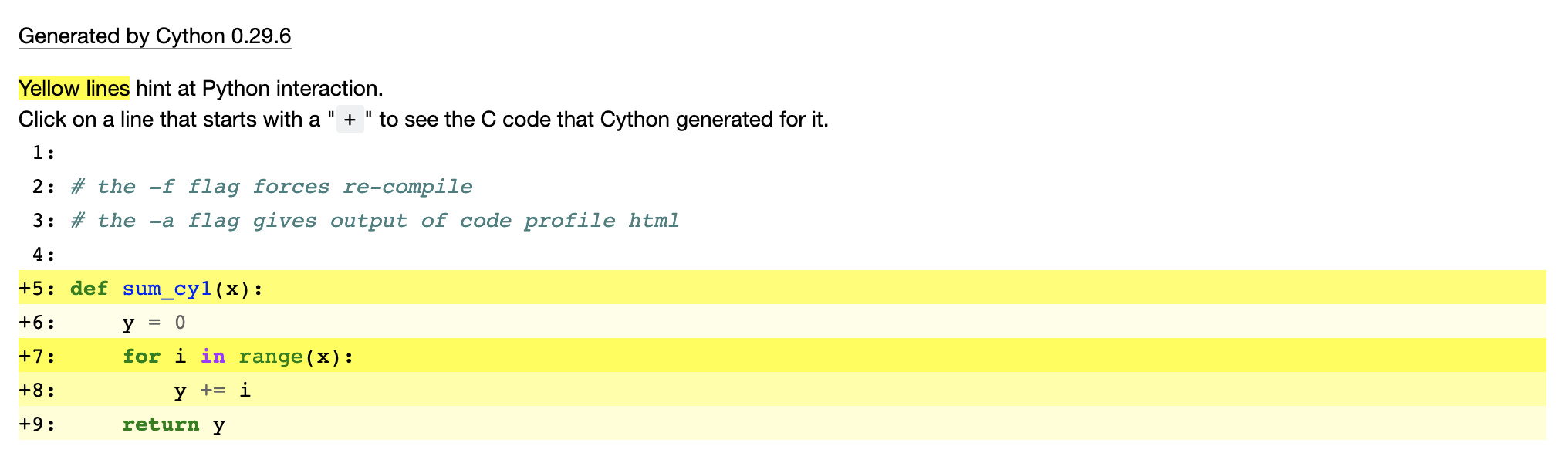
%%cython -f -a

# the -f flag forces re-compile
# the -a flag gives output of code profile html

def sum_cy1(x):
    y = 0
    for i in range(x):
        y += i
    return y

%%timeit

sum_py(1000)

62.5 µs ± 1.56 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)

%%timeit

sum_cy1(1000)

37.6 µs ± 2.29 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)

We can see that the Cython function is already faster, even though we didn’t make any modifications to the code. Next, let’s define another Cython function sum_cy2 where we define the types of the variables y and i, and see that we can get an even faster function.

%%cython -f -a

cpdef int sum_cy2(int x):
    cdef int y = 0
    cdef int i
    for i in range(x):
        y += i
    return y

%%timeit

sum_cy2(1000)

177 ns ± 6.95 ns per loop (mean ± std. dev. of 7 runs, 10000000 loops each)

Executing as script

We can also write Cython code in .pyx files, and run the cythonizer to obtain a .c file, as well as a shared object .so file.

File structure

cython_examples
+–python_sum.py
+–cython_sum.pyx
+–setup.py

In the file python_sum.py:

def sum_py(x):
    y = 0
    for i in range(x):
        y += i
    return y

In the file cython_sum.pyx:

cpdef int sum_cy(int x):
    cdef int y = 0
    cdef int i
    for i in range(x):
        y += i
    return y

In the file setup.py:

from distutils.core import setup
from Cython.Build import cythonize

setup(ext_modules = cythonize('cython_sum.pyx'))

To build C/C++ file and C object file from cython_sum.pyx file, run

python setup.py build_ext --inplace

This will create the files cython_sum.c and cython_sum.cpython-36m-darwin.so in the cython_examples directory, as well as a build directory.

We can now import the sum_cy function the cython_sum.cpython-36m-darwin.so object as a python object as follows.

from cython_sum import sum_cy

%%timeit

sum_cy(1000)

174 ns ± 2.22 ns per loop (mean ± std. dev. of 7 runs, 10000000 loops each)

Sampling in Cython

Next we’ll explore sampling from a random distribution in Cython. One difficulty in implementing the Gibbs sampler for LDA is that it must iterate through every token of the corpus, form a probability distribution, and draw a single number from that distribution. The distributions must be formed in sequence (and not in parallel); this brings up the need for Cython. If we were drawing many numbers from a single distribution, numpy would be a great, fast option, but the unique structure of this model pushes us out of that nice situation. Let’s walk through a few sampler functions to compare execution speeds.

# choose random distribution
p = np.random.rand(10)
p = p/p.sum()
p

array([0.19128002, 0.12793938, 0.13950299, 0.0326022 , 0.16675868,
       0.01937576, 0.14768875, 0.07719516, 0.09180864, 0.00584843])

def sample_py(p, n_samples):
    samples = np.zeros(shape=n_samples, dtype='int')
    a = range(p.shape[0])

    for i in range(n_samples):
        samples[i] = np.random.choice(a=a, p=p, size=None)

    return samples

%%timeit

samples = sample_py(p=p, n_samples=1000)

23.9 ms ± 2.6 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

%%cython -f -a

import numpy as np
cimport numpy as np

cpdef sample_cy(
    np.ndarray[np.float64_t, ndim=1] p,
    int n_samples
):
    samples = np.zeros(shape=n_samples, dtype='int')
    cdef np.ndarray[np.int64_t, ndim=1] a = np.array(range(p.shape[0]), dtype='int')

    for i in range(n_samples):
        samples[i] = np.random.choice(a=a, p=p, size=None)

    return samples

%%timeit

samples = sample_cy(p=p, n_samples=1000)

15.7 ms ± 345 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

a = range(p.shape[0])

%%timeit

samples = np.random.choice(a=a, p=p, size=1000)

59.4 µs ± 4.23 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)

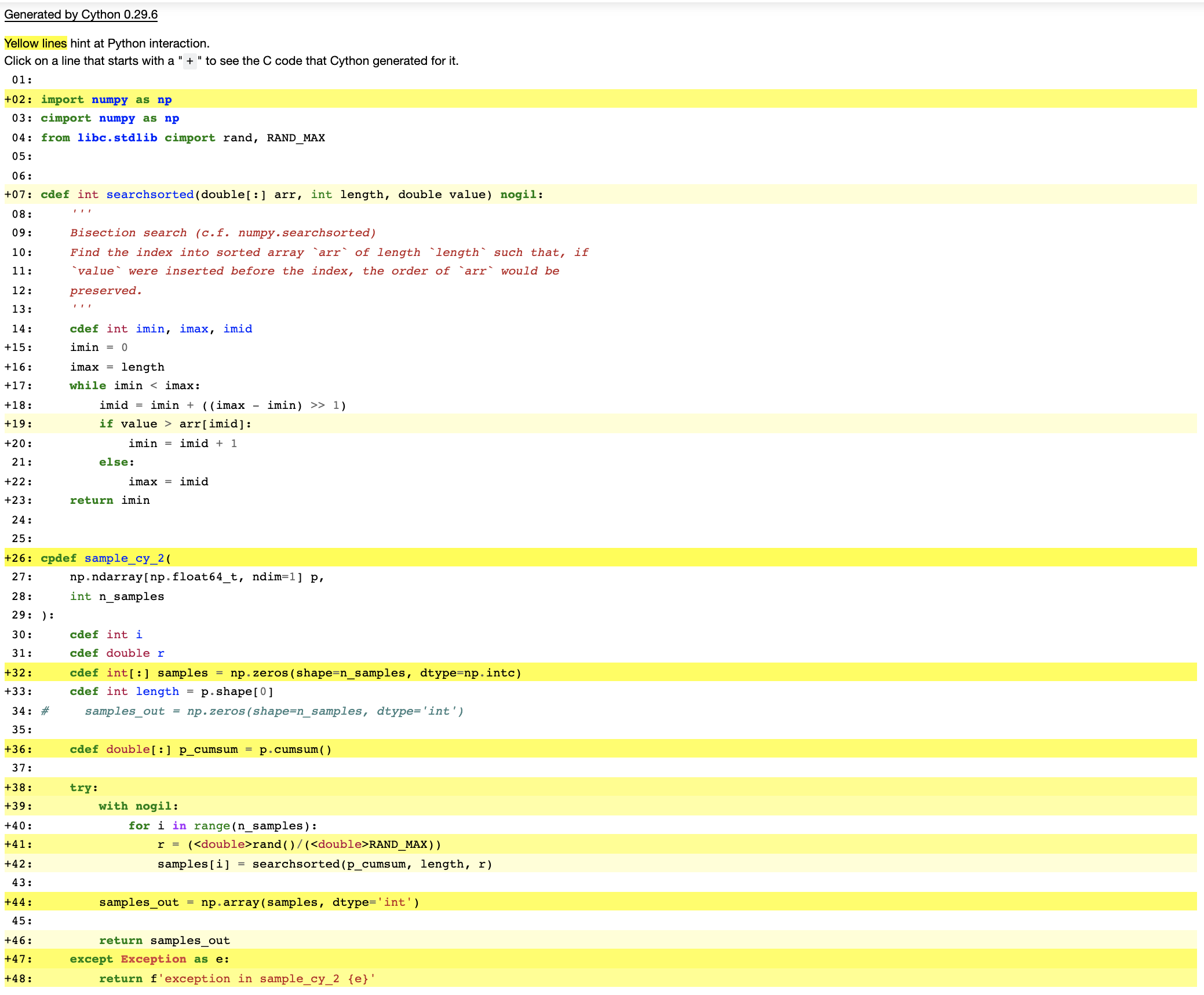
%%cython -f -a

import numpy as np
cimport numpy as np
from libc.stdlib cimport rand, RAND_MAX


cdef int searchsorted(double[:] arr, int length, double value) nogil:
    '''
    Bisection search (c.f. numpy.searchsorted)
    Find the index into sorted array `arr` of length `length` such that, if
    `value` were inserted before the index, the order of `arr` would be
    preserved.
    '''
    cdef int imin, imax, imid
    imin = 0
    imax = length
    while imin < imax:
        imid = imin + ((imax - imin) >> 1)
        if value > arr[imid]:
            imin = imid + 1
        else:
            imax = imid
    return imin


cpdef sample_cy_2(
    np.ndarray[np.float64_t, ndim=1] p,
    int n_samples
):
    cdef int i
    cdef double r
    cdef int[:] samples = np.zeros(shape=n_samples, dtype=np.intc)
    cdef int length = p.shape[0]

    cdef double[:] p_cumsum = p.cumsum()

    try:
        with nogil:
            for i in range(n_samples):
                r = (<double>rand()/(<double>RAND_MAX))
                samples[i] = searchsorted(p_cumsum, length, r)

        samples_out = np.array(samples, dtype='int')

        return samples_out
    except Exception as e:
        return f'exception in sample_cy_2 {e}'

%%timeit

samples = sample_cy_2(p=p, n_samples=1000)

34.1 µs ± 4.85 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)

LDA in Cython

We implement LDA using collapsed Gibbs sampling. For this, the output of the model is a topic assignment for each occurrence of each word in the corpus.

\[\begin{aligned} W& - \text{number of words in corpus (unique count)}\\ D& - \text{number of documents in corpus}\\ T& - \text{number of topics}\\ C^{WT}& - \text{word-topic count matrix}\\ C^{DT}& - \text{document-topic count matrix}\\ \beta& - \text{parameter for word topic prior}\\ \alpha& - \text{parameter for topic document prior} \end{aligned}\]

First, topic assignemnts are randomly initialized. This model is updated iteratively in the following way. For each word $w$ in the corpus, let $t$ be the topic currently assigned to $w$, and $d$ be the document $w$ is in.

Decrement $C^{WT}_{w, t}$ by 1
Decrement $C^{DT}_{d, t}$ by 1
Form the distribution over topics ${\bf z} = z_1, z_2, …, z_T$

\[P(z_j) \varpropto \frac{C^{WT}_{w, j}+\beta}{\sum\limits_{w=1}^W C^{WT}_{w, j} + W\beta} \frac{C^{DT}_{d, j}+\alpha}{\sum\limits_{t=1}^{T}C^{DT}_{d, t}+T\alpha}\]

Draw from $P({\bf z})$ to get new topic $t’$
Increment $C^{WT}_{w, t’}$ by 1
Increment $C^{DT}_{d, t’}$ by 1

corpus = [
    'i like to code python and cython for data science',
    'cython is pretty cool',
    'cython is super fast and fun',
    'lda in cython for data science is cool',
]

corpus_processed = [doc.split() for doc in corpus]

label_encoder = LabelEncoder()

label_encoder.fit(list(set.union(*[set(doc) for doc in corpus_processed])))

LabelEncoder()

corpus_processed = [label_encoder.transform(doc) for doc in corpus_processed]

corpus_processed

[array([ 8, 12, 17,  1, 14,  0,  3,  6,  4, 15]),
 array([ 3, 10, 13,  2]),
 array([ 3, 10, 16,  5,  0,  7]),
 array([11,  9,  3,  6,  4, 15, 10,  2])]

alpha = 10
beta = 0.01

token_count = 0
for doc in corpus_processed:
    token_count += len(doc)

Nw = np.zeros(shape=token_count, dtype='int')
Nd = np.zeros(shape=token_count, dtype='int')

# fill Nw and Nd
token_index = 0
for doc_idx, doc in enumerate(corpus_processed):
    for word_id in doc:
        Nw[token_index] = word_id
        Nd[token_index] = doc_idx
        token_index += 1

W = len(set(Nw)) # number of words
D = len(set(Nd)) # number of documents
K = 2 # number of topics

# randomly initialize topic assignments
Nz = np.random.randint(low=0, high=K, size=token_count, dtype='int')

nzw = np.zeros(shape=(K, W), dtype='int') # topic word count matrix
ndz = np.zeros(shape=(D, K), dtype='int') # document topic count matrix

# fill ndz and nzw
for i in range(token_count):
    d = Nd[i]
    w = Nw[i]
    z = Nz[i]
    ndz[d, z] += 1
    nzw[z, w] += 1

Nw
Nd
Nz
ndz
nzw

array([ 8, 12, 17,  1, 14,  0,  3,  6,  4, 15,  3, 10, 13,  2,  3, 10, 16,
        5,  0,  7, 11,  9,  3,  6,  4, 15, 10,  2])

array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3,
       3, 3, 3, 3, 3, 3])

array([1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0,
       1, 1, 1, 1, 0, 1])

array([[5, 5],
       [3, 1],
       [1, 5],
       [2, 6]])

array([[1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0],
       [1, 1, 1, 3, 1, 1, 1, 0, 1, 0, 2, 1, 1, 0, 0, 1, 1, 1]])

def sample_topics(
    Nw,
    Nd,
    Nz,
    ndz,
    nzw,
    K,
    W,
    alpha,
    beta,
):
    N = len(Nw)
    for i in range(N):
        w = Nw[i]
        d = Nd[i]
        z = Nz[i]

        # increment nzw and ndz
        nzw[z, w] -= 1
        ndz[d, z] -= 1

        denom_a = np.sum(ndz[d,:]) + K*alpha # number of tokens in document + K*alpha
        denom_b = nzw.sum(axis=1) + W*beta # number of tokens in each topic + # of words in vocab * beta

        # calculating probability word belongs to each topic
        p_z = ((nzw[:,w] + beta) / denom_b) * ((ndz[d,:] + alpha) / denom_a)

        # draw topic for word n from multinomial using probabilities calculated above
        z_new = np.random.choice(a=range(K), p=p_z/np.sum(p_z), size=None)

        # assign new topic to word
        Nz[i] = z_new

        # decrement nzw and ndz
        nzw[z_new, w] += 1
        ndz[d, z_new] += 1

def fit(
    iterations,
    Nw,
    Nd,
    Nz,
    ndz,
    nzw,
    K,
    W,
    alpha,
    beta,    
):
    for iteration in range(iterations):
        sample_topics(
            Nw=Nw,
            Nd=Nd,
            Nz=Nz,
            ndz=ndz,
            nzw=nzw,
            K=K,
            W=W,
            alpha=alpha,
            beta=beta,
        )

    return Nz

%%time

fit(
    iterations=100,
    Nw=Nw,
    Nd=Nd,
    Nz=Nz,
    ndz=ndz,
    nzw=nzw,
    K=K,
    W=W,
    alpha=alpha,
    beta=beta,
)

CPU times: user 174 ms, sys: 4.73 ms, total: 179 ms
Wall time: 176 ms

array([0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0,
       0, 0, 1, 1, 1, 0])

%%cython -f

import numpy as np
cimport numpy as np

cpdef sample_topics_(
    int[:] Nw,
    int[:] Nd,
    int[:] Nz,
    int[:, :] ndz,
    int[:, :] nzw,
    int[:] nz,
    int K,
    int W,
    double alpha,
    double beta,
):
    cdef int N = len(Nw)
    cdef int w, d, z, i, z_new
    cdef double[:] p_z = np.zeros(shape=K, dtype=np.float64)

    try:
        for i in range(N):
            w = Nw[i]
            d = Nd[i]
            z = Nz[i]

            # decrement nzw, ndz and nz
            nzw[z, w] -= 1
            ndz[d, z] -= 1
            nz[z] -= 1

            # calculating probability word belongs to each topic
            for k in range(K):
                # beta is a double so cdivision yields a double
                p_z[k] = (nzw[k, w] + beta) / (nz[k] + beta) * (ndz[d, k] + alpha)

            # draw topic for word n from multinomial using probabilities calculated above
            z_new = np.random.choice(a=range(K), p=p_z/np.sum(p_z), size=None)

            # assign new topic to word
            Nz[i] = z_new

            # increment nzw, ndz and nz
            nzw[z_new, w] += 1
            ndz[d, z_new] += 1
            nz[z_new] += 1

    except Exception as e:
        return f'Exception in _sample_topics: {e}'


cpdef fit_(
    int iterations,
    np.ndarray[np.int64_t, ndim=1] Nw_in,
    np.ndarray[np.int64_t, ndim=1] Nd_in,    
    np.ndarray[np.int64_t, ndim=1] Nz_in,
    np.ndarray[np.int64_t, ndim=2] ndz_in,
    np.ndarray[np.int64_t, ndim=2] nzw_in,
    int K,
    int W,
    double alpha,
    double beta,
):
    cdef int it, idx
    cdef int token_count = len(Nw_in)
    Nt_np_arr = np.zeros(shape=token_count, dtype='int')
    nz = np.zeros(shape=K, dtype='int')

    try:
        Nw = Nw_in.astype(np.intc)
        Nd = Nd_in.astype(np.intc)
        Nz = Nz_in.astype(np.intc)
        nzw = nzw_in.astype(np.intc)
        ndz = ndz_in.astype(np.intc)

        for idx_wt, val_wt in enumerate(nzw.sum(axis=1)):
            nz[idx_wt] = val_wt

        nz = nz.astype(np.intc)

        for it in range(iterations):
            sample_topics_(
                Nw=Nw,
                Nd=Nd,
                Nz=Nz,
                nzw=nzw,
                ndz=ndz,
                nz=nz,
                K=K,
                W=W,
                alpha=alpha,
                beta=beta,
            )

        for idx in range(token_count):
            Nt_np_arr[idx] = Nz[idx]

        return Nt_np_arr  

    except Exception as e:
        return f'Exception in fit: {e}'

%%time

fit_(
    iterations=100,
    Nw_in=Nw,
    Nd_in=Nd,
    Nz_in=Nz,
    ndz_in=ndz,
    nzw_in=nzw,
    K=K,
    W=W,
    alpha=alpha,
    beta=beta,
)

CPU times: user 147 ms, sys: 26.8 ms, total: 174 ms
Wall time: 154 ms

array([1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1,
       0, 1, 1, 1, 1, 1])

%%cython -f

import numpy as np
cimport numpy as np
from libc.stdlib cimport rand, RAND_MAX
from cython.operator cimport preincrement as inc, predecrement as dec



cdef int searchsorted(double[:] arr, int length, double value) nogil:
    '''
    Bisection search (c.f. numpy.searchsorted)
    Find the index into sorted array `arr` of length `length` such that, if
    `value` were inserted before the index, the order of `arr` would be
    preserved.
    '''
    cdef int imin, imax, imid
    imin = 0
    imax = length
    while imin < imax:
        imid = imin + ((imax - imin) >> 1)
        if value > arr[imid]:
            imin = imid + 1
        else:
            imax = imid
    return imin


cpdef sample_topics_2_(
    int[:] Nw,
    int[:] Nd,
    int[:] Nz,
    int[:, :] ndz,
    int[:, :] nzw,
    int[:] nz,
    int K,
    int W,
    double alpha,
    double beta,
):
    cdef int N = len(Nw)
    cdef int w, d, z, i, z_new
    cdef double r, dist_cum
    cdef double[:] dist_sum = np.zeros(shape=K, dtype=np.float64)

    try:
        with nogil:
            for i in range(N):
                w = Nw[i]
                d = Nd[i]
                z = Nz[i]

                # decrement nzw, ndz and nz
                dec(nzw[z, w])
                dec(ndz[d, z])
                dec(nz[z])

                # calculating probability word belongs to each topic
                dist_cum = 0
                for k in range(K):
                    # beta is a double so cdivision yields a double
                    dist_cum += (nzw[k, w] + beta) / (nz[k] + beta) * (ndz[d, k] + alpha)
                    dist_sum[k] = dist_cum

                # draw topic for word n from multinomial using probabilities calculated above
                r = (<double>rand()/(<double>RAND_MAX)) * dist_cum # dist_cum == dist_sum[-1]
                z_new = searchsorted(dist_sum, K, r)

                # assign new topic to word
                Nz[i] = z_new

                # increment nzw and ndz
                inc(nzw[z_new, w])
                inc(ndz[d, z_new])
                inc(nz[z_new])

    except Exception as e:
        return f'Exception in _sample_topics: {e}'


cpdef fit_2_(
    int iterations,
    np.ndarray[np.int64_t, ndim=1] Nw_in,
    np.ndarray[np.int64_t, ndim=1] Nd_in,    
    np.ndarray[np.int64_t, ndim=1] Nz_in,
    np.ndarray[np.int64_t, ndim=2] ndz_in,
    np.ndarray[np.int64_t, ndim=2] nzw_in,
    int K,
    int W,
    double alpha,
    double beta,
):
    cdef int it, idx
    cdef int token_count = len(Nw_in)
    Nt_np_arr = np.zeros(shape=token_count, dtype='int')
    nz = np.zeros(shape=K, dtype='int')

    try:
        Nw = Nw_in.astype(np.intc)
        Nd = Nd_in.astype(np.intc)
        Nz = Nz_in.astype(np.intc)
        nzw = nzw_in.astype(np.intc)
        ndz = ndz_in.astype(np.intc)

        for idx_wt, val_wt in enumerate(nzw.sum(axis=1)):
            nz[idx_wt] = val_wt

        nz = nz.astype(np.intc)

        for it in range(iterations):
            sample_topics_2_(
                Nw=Nw,
                Nd=Nd,
                Nz=Nz,
                nzw=nzw,
                ndz=ndz,
                nz=nz,
                K=K,
                W=W,
                alpha=alpha,
                beta=beta,
            )

        for idx in range(token_count):
            Nt_np_arr[idx] = Nz[idx]

        return Nt_np_arr  

    except Exception as e:
        return f'Exception in fit: {e}'

%%time

fit_2_(
    iterations=100,
    Nw_in=Nw,
    Nd_in=Nd,
    Nz_in=Nz,
    ndz_in=ndz,
    nzw_in=nzw,
    K=K,
    W=W,
    alpha=alpha,
    beta=beta,
)

CPU times: user 1.98 ms, sys: 1.34 ms, total: 3.32 ms
Wall time: 2.21 ms

array([0, 0, 2, 2, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1,
       0, 1, 1, 0, 1, 0])

import pickle

with open('bbc_corpus.pickle', 'rb') as f:
    bbc_corpus = pickle.load(f)

label_encoder = LabelEncoder()

label_encoder.fit(list(set.union(*[set(doc) for doc in bbc_corpus])))

LabelEncoder()

%%time

corpus_processed = [label_encoder.transform(doc) for doc in bbc_corpus]

CPU times: user 4.23 s, sys: 39.3 ms, total: 4.27 s
Wall time: 4.27 s

alpha = 10
beta = 0.01

token_count = 0
for doc in corpus_processed:
    token_count += len(doc)

Nw = np.zeros(shape=token_count, dtype='int')
Nd = np.zeros(shape=token_count, dtype='int')

# fill Nw and Nd
token_index = 0
for doc_idx, doc in enumerate(corpus_processed):
    for word_id in doc:
        Nw[token_index] = word_id
        Nd[token_index] = doc_idx
        token_index += 1

W = len(set(Nw)) # number of words
D = len(set(Nd)) # number of documents
K = 5 # number of topics

# randomly initialize topic assignments
Nz = np.random.randint(low=0, high=K, size=token_count, dtype='int')

nzw = np.zeros(shape=(K, W), dtype='int') # topic word count matrix
ndz = np.zeros(shape=(D, K), dtype='int') # document topic count matrix

# fill ndz and nzw
for i in range(token_count):
    d = Nd[i]
    w = Nw[i]
    z = Nz[i]
    ndz[d, z] += 1
    nzw[z, w] += 1

Nw
Nd
Nz
ndz
nzw

array([11161, 16337, 13575, ..., 15447,  4798,  9390])

array([   0,    0,    0, ..., 2224, 2224, 2224])

array([4, 3, 2, ..., 2, 4, 1])

array([[25, 32, 38, 28, 54],
       [81, 77, 83, 77, 70],
       [33, 40, 34, 37, 35],
       ...,
       [36, 26, 31, 22, 27],
       [32, 51, 38, 26, 30],
       [20, 17, 19, 21, 14]])

array([[ 6,  1,  0, ...,  1,  0, 23],
       [ 7,  0,  1, ...,  0,  0, 22],
       [ 4,  1,  0, ...,  1,  2, 29],
       [ 6,  0,  0, ...,  1,  0, 28],
       [ 1,  2,  2, ...,  1,  0, 27]])

%%time

fit(
    iterations=10,
    Nw=Nw,
    Nd=Nd,
    Nz=Nz,
    ndz=ndz,
    nzw=nzw,
    K=K,
    W=W,
    alpha=alpha,
    beta=beta,
)

CPU times: user 5min 50s, sys: 3.05 s, total: 5min 53s
Wall time: 5min 53s

array([0, 1, 0, ..., 3, 0, 4])

%%time

fit_2_(
    iterations=10,
    Nw_in=Nw,
    Nd_in=Nd,
    Nz_in=Nz,
    ndz_in=ndz,
    nzw_in=nzw,
    K=K,
    W=W,
    alpha=alpha,
    beta=beta,
)

CPU times: user 321 ms, sys: 2.39 ms, total: 323 ms
Wall time: 322 ms

array([2, 4, 3, ..., 2, 2, 2])

We can see that the implementation of the collapsed Gibbs sampler for LDA using Cython is much faster than the implementation in Python using numpy.